Dragi posjetitelji, drago nam je da vas je naša slika zainteresirala.
Jeste li ikada čuli riječ geometrija? Znate li što ona znači? Riječ geometrija dolazi od grčke riječi koja u prijevodu znači zemljomjerstvo, odnosno geometrija se je počela razvijati kao vještina mjerenja zemlje. Iako je danas geometrija samo jedan dio matematike priče o nastanku geometrije zapravo je priča o nastanku matematike jer razvoj matematike započeo je razvojem geometrije. Nadamo se da ste spremni za priču o geometrijama…
Priča o geometrijama započinje još u starom Egiptu te iz tog vremena dolazi i sam naziv geometrija – mjerenje zemlje. Egipćani su, kako je bilo i uobičajeno u to doba, geometriju razvijali zbog svakodnevnih potreba, npr. svake godine, nakon poplave Nila, bilo je potrebno ponovo podijeliti zemlju i ucrtati granice zemljišnih posjeda. Iako smo zadržali naziv, definirati geometriju kao granu matematike uopće nije jednostavno. Samim matematičarima trebalo je oko 2000 godina da geometriju postave na noge. Sve je započelo s Euklidom i njegovim Elementima u kojim je on pokušao opisati geometriju, upravo onu koju su još u starom Egiptu koristili. Kao što danas zakonima definiramo pravila ponašanja i odnosne među ljudima te odnose među ljudima i nekim drugim kategorijama (npr. nekretnine i pokretnine), tako je i Euklid pokušao dati pravila ponašanja za elemente (točke i pravce) koji „žive“ u geometriji te za odnose među njima. Ta pravila ponašanja zovemo aksiomima ili postulatima. Euklid je svoje geometrijske zakone postavio oko 300. godine prije nove ere u Elementima. Zanimljiv je podatak da je samo Biblija izdana u više izdanja od Euklidovih Elemenata. Brojni matematičari nakon Euklida nastavili su njegov rad, ali su ga i mnogi kritizirali. Najviše je ”buke” digao njegov poznati 5. postulat za kojega su mnogi smatrali da mu nije mjesto među postulatima već da je on posljedica drugih postulata.
I da ako dužina koja siječe dvije dužine čini unutarnje kutove s iste strane manjima od pravog kuta, dvije dužine, neograničeno produžene, sastaju se s one strane na kojoj su kutovi manji od dva prava kuta.
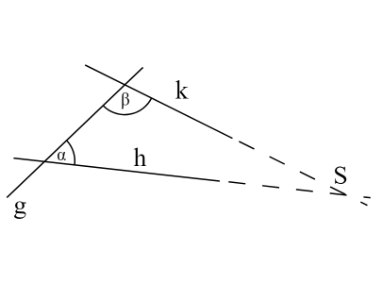
I nama matematičarima malo je neobičan Euklidov jezik pa često njegov postulat iskazujemo drugim riječima, na sljedeći način.
Neka je T točka koja ne pripada pravcu p: Tada postoji jedinstveni pravac q koji sadrži točku T i paralelan je s pravcem p.
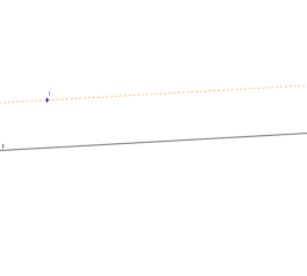
Promišljanje velikog broja matematičara nakon Euklida o dobrim i lošim stranama Euklidovih Elementa s vremenom je dovelo do revolucionarnog rezultata u matematici. Ako možemo govoriti o otkrićima u matematici, onda je ovo sigurno među top 3 otkrića u matematici. U prvoj polovi 19. stoljeća dva su matematičara (nezavisno) otkrili novu geometriju. Njihova imena su Bolyai i Lobačevski, a tu geometriju danas zovemo hiperbolička geometrija. To nije geometrija koju je Euklid opisao u svojim Elementima te se ona ne ponaša prema pravilima koje je Euklid dao, niti su ju koristili u starom Egiptu. Taj je rezultat dao vjetar u leđa razvoju geometrije i ono što danas nazivamo geometrijom puno je šire od onoga što je Euklid smatrao pod pojmom geometrija. Tu njegovu geometriju danas, njemu u čast, zovemo euklidska geometrija.
Ali da završimo priču o Euklidu… 1899. godine veliki matematičar Hilbert zaokružuje priču o euklidskoj ravninskoj geometriji. Priča je to koja ima puno koautora, ali Euklid je ipak najveća faca među njima. Trebalo je oko 2000 godina, ali nepravda je ispravljena. Iako je Euklidov opis geometrije imao nedostataka, svi oni koji su kritizirali njegov 5. postulat bili su u krivu. Geometrija koju učimo u školi i na većini studija euklidska je geometrija.
Nadamo se da ste uživali u našoj kratkoj priči o geometrijama. Ako smo vas zainteresirali i želite pročitati nešto više, slijedite sljedeće poveznice:
http://e.math.hr/math_e_article/vol22/Crnkovic
https://www.mathos.unios.hr/~mdjumic/uploads/diplomski/BOG23.pdf